Week 5 Assignment: Understanding Normal Distribution
Q1
Rosetta averages 148 points per bowling game with a standard deviation of 14 points. Suppose Rosetta’s points per bowling game are normally distributed. Let X= the number of points per bowling game. Then X∼N(148,14).
If necessary, round to three decimal places.
Q2
Suppose X∼N(12.5,1.5), and x=11. Find and interpret the z-score of the standardized normal random variable.
Q3
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.
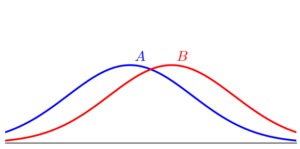
Ans:
A has the larger mean.
B has the larger mean.
The means of A and B are equal.
A has the larger standard deviation.
B has the larger standard deviation.
The standard deviations of A and B are equal.
Q4
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.
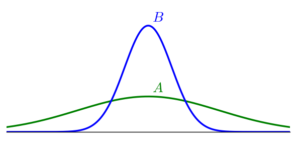
Ans:
A has the larger mean.
B has the larger mean.
The means of A and B are equal.
A has the larger standard deviation.
B has the larger standard deviation.
The standard deviations of A and B are equal.
Q5
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.
Ans:
A has the larger mean.
B has the larger mean.
The means of A and B are equal.
A has the larger standard deviation.
B has the larger standasrd deviation.
The standard deviations of A and B are equal.
Q6
The graph below shows the graphs of several normal distributions, labeled A, B, and C, on the same axis. Determine which normal distribution has the smallest mean.
Q7
Hugo averages 22 points per basketball game with a standard deviation of 4 points. Suppose Hugo’s points per basketball game are normally distributed. Let X= the number of points per basketball game. Then X∼N(22,4).
Q8
Gail averages 64 words per minute on a typing test with a standard deviation of 9.5 words per minute. Suppose Gail’s words per minute on a typing test are normally distributed. Let X= the number of words per minute on a typing test. Then X∼N(64,9.5).
If necessary, round to three decimal places.
Q9
n 2014, the CDC estimated that the mean height for adult women in the U.S. was 64 inches with a standard deviation of 4 inches. Suppose X, height in inches of adult women, follows a normal distribution. Let x=68, the height of a woman who is 5′ 8″ tall. Find and interpret the z-score of the standardized normal random variable.
Ans:
This means that x=68 is one standard deviation (1σ) above or to the right of the mean, μ=64.
This means that x=68 is two standard deviations (2σ) above or to the right of the mean, μ=64.
This means that x=68 is three standard deviations (3σ) above or to the right of the mean, μ=64.
This means that x=68 is one standard deviation (1σ) below or to the left of the mean, μ=64.
This means that x=68 is two standard deviations (2σ) below or to the left of the mean, μ=64.
This means that x=68 is three standard deviations (3σ) below or to the left of the mean, μ=64.
Q10
John averages 58 words per minute on a typing test with a standard deviation of 11 words per minute. Suppose John’s words per minute on a typing test are normally distributed. Let X= the number of words per minute on a typing test. Then X∼N(58,11).
If necessary, round to three decimal places.
Q11
Lexie averages 149 points per bowling game with a standard deviation of 14 points. Suppose Lexie’s points per bowling game are normally distributed. Let X= the number of points per bowling game. Then X∼N(149,14).
If necessary, round to three decimal places.
Q12
Isabella averages 152 points per bowling game with a standard deviation of 14.5 points. Suppose Isabella’s points per bowling game are normally distributed. Let X= the number of points per bowling game. Then X∼N(152,14.5).
If necessary, round to three decimal places.
Q13
Annie averages 23 points per basketball game with a standard deviation of 4 points. Suppose Annie’s points per basketball game are normally distributed. Let X= the number of points per basketball game. Then X∼N(23,4).
Solution
Q1
Rosetta averages 148 points per bowling game with a standard deviation of 14 points. Suppose Rosetta’s points per bowling game are normally distributed. Let X= the number of points per bowling game. Then X∼N(148,14).
If necessary, round to three decimal places.
Ans:
Suppose Rosetta scores 110 points in the game on Thursday. The z-score when x=110 is −2.714. The mean is $$148.
This z-score tells you that x=110 is 2.714 standard deviations to the left of the mean.
Q2
Suppose X∼N(12.5,1.5), and x=11. Find and interpret the z-score of the standardized normal random variable.
Ans:
The z-score when x=11 is −1. The mean is 12.5.
This z-score tells you that x=11 is 1 standard deviation(s) to the left of the mean.………..please follow the link below to purchase the solutions at just $5
Question
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.
Question
Lexie averages 149 points per bowling game with a standard deviation of 14 points. Suppose Lexie’s points per bowling game are normally distributed. Let X= the number of points per bowling game. Then X∼N(149,14). If necessary, round to three decimal places.
Question
Suppose X∼N(12.5,1.5), and x=11. Find and interpret the z-score of the standardized normal random variable.
Question
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.
Question
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.
Question
Given the plot of normal distributions A and B below, which of the following statements is true? Select all correct answers.
Question
Rosetta averages 148 points per bowling game with a standard deviation of 14 points. Suppose Rosetta’s points per bowling game are normally distributed. Let X= the number of points per bowling game. Then X∼N(148,14).
If necessary, round to three decimal places.
Question
Suppose X∼N(16.5,0.5), and x=16. Find and interpret the z-score of the standardized normal random variable.
Solution
Question
Lexie averages 149 points per bowling game with a standard deviation of 14 points. Suppose Lexie’s points per bowling game are normally distributed. Let X= the number of points per bowling game. Then X∼N(149,14). If necessary, round to three decimal places.
Answer: Suppose Lexie scores 186 points in the game on Tuesday. The z-score when x = 186 is 2. 643. The mean is 149…
Question
Suppose X∼N(12.5,1.5), and x=11. Find and interpret the z-score of the standardized normal random variable.
Answer: The z-score when x=11 is negative -1 The mean is 2……………………………….please follow the link below to purchase the solution at $5
